中点的性质前沿信息_中点的性质是什么(2024年11月实时热点)
三角形五心总结:公式与性质全解析 你是否还记得三角形的五心呢?” 如果突然在题目中看到“点O是三角形的内心”,你可能会感到困惑。别担心,今天我们来总结一下这五个心的性质,帮你巩固记忆! 1️⃣ 重心:三角形三边串线的交点。 性质1:重心到三角形三边的距离相等。 性质2:三角形的重心到任意一边的中点的距离是该边的一半。 性质3:若三角形的三边为a、b、c,则重心的坐标为((a+b+c)/3, (a+b+c)/3)。 2️⃣ 外心:三角形三边中垂线的交点,即外接圆圆心。 性质1:外心到三角形的三个顶点的距离相等。 性质2:若三角形的一个角为直角,则外心到该直角的两边的距离之和等于该直角的一半。 性质3:设三角形的三边为a、b、c,则外接圆的半径R可以通过海伦公式计算:R = (abc)/(4S)。 3️⃣ 内心:三角形三条角平分线的交点,即内切圆圆心。 性质1:内心到三角形三边的距离相等。 性质2:内心到三角形三个顶点的距离之和等于三角形周长的一半。 性质3:设三角形的三边为a、b、c,则内切圆的半径r可以通过内切半径公式计算:r = (S/L) 㗠P。 4️⃣ 旁心:三角形一个内角的平分线与其他两个内角的外角平分线的交点。 性质1:三角形有三个旁心。 性质2:旁心一定在三角形外部。 性质3:旁心到三角形三边的距离相等。 性质4:旁心到三角形三个顶点的距离之和等于三角形周长的一半。 5️⃣ 垂心:三角形三条高的交点。 性质1:三角形任一顶点到的距离等于外心到对边的距离的两倍。 性质2:垂心到三角形三个顶点的距离之和等于三角形周长的一半。 注意:等边三角形的重心、外心、内心和垂心是同一点,称为中心。中心同时具有四心的性质。 希望这份总结能帮助你更好地理解和记忆三角形的五心!ꀀ
三角形五心详解及其性质定理 三角形五心及相关定理是初中数学的重要知识点,也是中考数学几何模型的常见考点。以下是三角形五心的详细总结及其相关性质定理。 Œ 一重心 定义:三角形三边中线的交点。 性质:重心将每条中线分为2:1的比例。 公式:$BC^2 = 2(AB^2 + AC^2)$。 结论:重心到三角形任意一边的中点连线,与该边平行且等于该边的一半。 Œ 二垂心 定义:三角形三垂线的交点。 性质:垂心与三角形的三个顶点组成垂心组。 结论:垂心到三角形任意一边的垂线,与该边垂直且等于该边的一半。 Œ 三外心 定义:三角形三达中垂线的交点。 性质:外心是三角形的外接圆圆心。 公式:$R = \frac{a}{2\sin A} = \frac{b}{2\sin B} = \frac{c}{2\sin C}$。 结论:外心到三角形任意一边的距离等于该边的长度除以该边对应的正弦值。 Œ 四内心 定义:三角形三条内平公线的交点。 性质:内心是三角形的内切圆圆心。 公式:$r = \frac{2S}{a + b + c}$。 结论:内心到三角形任意一边的距离等于该边的长度乘以该边对应的正弦值的一半,再除以三角形的周长。 Œ 五旁心 定义:三角形一内向平与外两外线的交点。 性质:旁心在三角形内部,且到三角形任意一边的距离等于该边的长度除以该边对应的正弦值的一半。 Œ 欧拉线 结论:重心、外心、垂心三点共线,且重心到垂心的距离等于外心到垂心的距离的两倍。 Œ 五点共圆 结论:重心、外心、内心、垂心在三角形中五点共圆,且这个圆的半径等于外接圆半径的一半。 通过以上总结,我们可以更好地理解和掌握三角形五心的性质和定理,为解决相关数学问题打下基础。
š 初二上册数学重点攻略 – 三角形的高、中线与角平分线,你掌握了吗? 探索三角形的奥秘,从基础开始! 1️⃣ 三角形的高:从三角形的一个顶点向对边作垂线,这条垂线就是三角形的高。 2️⃣ 三角形的中线:连接三角形的一个顶点和它对边的中点,这条线段就是三角形的中线。 3️⃣ 三角形的角平分线:从一个角的顶点出发,将这个角平分,这条射线就是三角形的角平分线。 ᠩ€š过这些知识点,我们可以更深入地了解三角形的性质和特点。快来一起学习吧! š 掌握这些知识点,不仅能帮助你更好地理解数学,还能在实际生活中应用。比如,在建筑、测量等领域,三角形的高、中线和角平分线都是非常重要的概念。 ꠥŠ 油,让我们一起成为数学小达人!
š 四点共圆的证明方法与判定技巧 四点共圆的基本性质 四点共圆时,圆内接四边形的对角互补,即角度和为180度。 如果四个点到某个点的距离相等,那么这四个点共圆。 如果一个四边形的外角等于其内对角,那么这四个点共圆。 Œ 判定方法 如果一个四边形的一组对角互补,那么这四个点共圆。 如果两个点在一条线段同旁,并且这条线段两端连线所夹的角相等,那么这两个点和这条线段的两个端点共圆。 如果同斜边的两个三角形顶点共线,那么这三个点共圆。 – 示例与证明 在等边三角形ABC中,AB=6,P为AB上一动点,PDIBC于D,PEIAC于E,求DE的最小值。 思路:要求DE的最小值,可以利用垂径定理,找到与半径的关系。连接PD和PE,取中点M,连接DM和EM。当P点最小时,DE也最小。利用三角函数和等边三角形的性质,可以求出DE的最小值。 砨˜Ž技巧 利用同弧所对的圆周角相等原理,证明四点共圆。 利用四边形对角互补的性质,证明四点共圆。 利用外角等于内对角的性质,证明四点共圆。 š 通过这些性质和判定方法,我们可以轻松证明四点共圆的问题。希望这些技巧能帮助你更好地理解几何问题!
考试中那些书本里找不到的数学技巧 ### 倍长中线法 𘊥œ襤„理与三角形中线相关的问题时,一个非常实用的方法是“倍长中线法”。简单来说,就是把中线延长到和中线一样长,这样就会构造出一对“8字型”的全等三角形,问题也就迎刃而解了。 倍长中线法的推广形式 š 如果题目中没有明确提到三角形中线,但有中点出现,我们也可以尝试将与中点相连的线段延长一倍,然后利用三角形全等的性质来解决问题。 截长补短 ✂️ 截长补短其实有两种方法:截长法和补短法。简单来说,就是在某条线段上截取一段与特定线段相等,或者将某条线段延长使其与特定线段相等,然后再利用三角形全等的性质来证明。 使用场景 œ詢˜目条件或结论中,如果看到线段的和或差,可以考虑使用截长补短的方法。 四大名辅 利用角平分线构造对称型全等也是解决几何问题的一个有效方法。 角分线垂两边 在角平分线上找一个点,然后向角的一边或两边作垂线,这样可以构造出全等三角形。 角分线垂中间 当题目中有角平分线和与之垂直的线段时,可以延长这条线段与角的另一边相交,从而构造出全等三角形。 角分线分两边 ✖️ 以角平分线为轴将图形翻折,在角平分线两侧构造全等三角形。 角分线遇平行线 如果角平分线遇到平行线,那么等腰三角形必会出现。 这些方法虽然不是书本上直接提到的,但在考试中却非常实用。掌握这些技巧,可以在解决几何问题时更加得心应手。
š 初三数学知识点全解析(三) ### 平行线与三角形 平行线等分线段定理及其推论1、2 三角形、梯形的中位线定理 平行线间的距离处处相等(例如,找面积相等的三角形) 重要辅助线 常连结四边形的对角线 梯形中常“平移一腰”、“平移对角线”、“作高”、“连结顶点和对腰中点并延长与底边相交”转化为三角形 作图:任意等分线段 圆的基础知识 圆的定义 弦、直径;弧、等弧、优弧、劣弧、半圆;弦心距;等圆、同圆、同心圆等概念 “三点定圆”定理 垂径定理及其推论 “等对等”定理及其推论 与圆有关的角 圆心角定义(等对等定理) 圆周角定义(圆周角定理,与圆心角的关系) 弦切角定义(弦切角定理) 直线与圆的位置关系 三种位置及判定与性质:相离、相切、相交 切线的性质(重点) 切线的判定定理(重点) 圆的切线的判定方法 切线长定理 圆与圆的位置关系 五种位置关系及判定与性质(重点:相切) 外离、外切、相交、内切、内含 相切(交)两圆连心线的性质定理 两圆的公切线:定义和性质 与圆有关的比例线段 相交弦定理 切割线定理 正多边形与圆 圆的内接、外切多边形(三角形、四边形) 三角形的外接圆、内切圆及性质 圆的外切四边形、内接四边形的性质 正多边形及计算:中心角、内角的一半等 计算公式 圆周长公式 圆面积公式 扇形面积公式 弧长公式 弓形面积的计算方法 圆柱、圆锥的侧面展开图及相关计算 点的轨迹 六条基本轨迹 作图 作三角形的外接圆、内切圆 平分已知弧 作已知两线段的比例中项 等分圆周:4、8;6、3等分 基本图形与辅助线 作半径 见弦往往作弦心距 见直径往往作直径上的圆周角 切点圆心莫忘连 两圆相切公切线(连心线) 两圆相交公共弦
三角形和中位线定理的证明方法详解 ### 三角形中位线定理的证明 – 三角形中位线定理是几何中的重要定理之一,它可以帮助我们更方便地解决各种几何问题。下面我们来详细讲解一下这个定理的证明过程。 定义和辅助线作法 首先,我们定义一下三角形中位线定理:在三角形ABC中,如果点E是AB的中点,点F是AC的中点,那么EF就是三角形ABC的中位线,并且EF平行于BC,且等于BC的一半。 证明过程 为了证明这个定理,我们可以采用以下步骤: 连接BE和CF — 在三角形ABC中,连接BE和CF。由于E和F分别是AB和AC的中点,所以BE平行于AC,CF平行于AB。 利用平行线的性质 根据平行线的性质,我们知道BE平行于AC,所以角BEA等于角CAB。同理,CF平行于AB,所以角CFA等于角BAC。 证明EF平行于BC „ 由于角BEA等于角CAB,且角CFA等于角BAC,我们可以得出角BEF等于角CFE。根据同位角的性质,我们知道EF平行于BC。 证明EF等于BC的一半 最后,我们利用相似三角形的性质来证明EF等于BC的一半。由于BE平行于AC,CF平行于AB,所以三角形BEF相似于三角形ABC。根据相似三角形的性质,我们有EF等于BC的一半。 梯形中位线定理的证明 ꊊ梯形中位线定理的证明方法与三角形中位线定理类似。我们只需要连接梯形两腰的中点,然后利用平行线和相似三角形的性质来证明中位线的性质。具体步骤如下: 连接梯形两腰的中点 — 在梯形ABCD中,连接AE和BF。由于E和F分别是AB和BC的中点,所以AE平行于DC,BF平行于AC。 利用平行线的性质 根据平行线的性质,我们知道AE平行于DC,所以角AED等于角D。同理,BF平行于AC,所以角BFC等于角C。 证明EF平行于DC „ 由于角AED等于角D,且角BFC等于角C,我们可以得出角AEF等于角CFE。根据同位角的性质,我们知道EF平行于DC。 证明EF等于DC的一半 最后,我们利用相似三角形的性质来证明EF等于DC的一半。由于AE平行于DC,BF平行于AC,所以三角形AEF相似于三角形ABC。根据相似三角形的性质,我们有EF等于DC的一半。 总结 无论是三角形还是梯形,中位线定理的证明方法都离不开平行线和相似三角形的性质。通过这些性质,我们可以轻松地证明中位线的存在性和性质。希望这篇文章能帮助你更好地理解中位线定理的证明方法!
八上数学预习:30Ⱘ璧š„直角三角形详解 š 预习内容:30Ⱘ璧š„直角三角形 探索题目: 8️⃣ (原创题)如图,△ABC是等边三角形,D是AC的中点,E是BC延长线上一点,CE=CD,ED的延长线交AB于点F。 求证:EF⊥AB 求证:DE=2DF 9️⃣ (原创题)如图,在△ABC中,∠C=45Ⱟˆ A=15ⰯC的垂直平分线DE交BC于点D,交AC于点E,AB的垂直平分线FH交AB于点F,交AC于点H。 求证:DE⊥FH 求证:AH的值 Ÿ (2023原创题)如图,在△ABC中,AB=AC,∠BAC=120Ⱟ🇧‚𝜂C的垂线CD,连接AD交BC于点M。若BM=3CM,求证:AB=2CD。 ⠯021洪山区期中改)如图,在△ABC中,AB=AC,∠BAC=120Ⱟ‚€N在底边BC上,且∠ANB=45Ⱟˆ MAN=60Ⱓ€‚ 画出△AAMN关于直线AN对称的△AADN 求证:CN的值 „ 探索提示: 每道题目都涉及到了30Ⱘ璧š„直角三角形的性质和定理的应用。通过解决这些题目,你可以更好地理解直角三角形的性质和解题方法。记得在做题时仔细思考,尝试多种解题方法,这样可以帮助你更好地掌握数学知识和技能。加油!ꀀ
双曲线的几何性质与应用:从理论到实践 “ 两节课+听课+听讲座的组合,今天聚焦于双曲线的简单几何性质。原本计划深入探讨双曲线的第二定义、直线与双曲线的交点个数问题以及点差法中点弦问题,但考虑到学生们的基础和速度,我们决定先从第二定义和交点个数问题开始。虽然这可能会影响课时进度,但“进一寸有进一寸的欢喜”,慢慢来,总会有收获。如果再上一次这节课,我会提前布置题目让他们先做,这样今天就能节省一些时间,明天的课程也能更顺利。 ƒ♂️ 今天真是忙到飞起,专家们的声势浩大,他们的工作真是太棒了,让人羡慕不已。感觉今天把时间利用到了极致,越来越像个时间管理大师。不过,成年人要为自己的选择付出代价,保持心情愉快最重要。他强任他强,至少每天都把该做的事情做完了。这周基本每天都在锻炼身体,工作虽然累,但心态超好(真正的英雄主义是在看清生活的真相之后依然热爱生活)。成熟的打工人要学会自我PUA,希望明天也能快快乐乐,晚安咯䊊š 理论很好,但如何检验理论的可行性呢?那就看看能不能实操吧。理论能运用于实践就是好的理论。很显然,高中学生日益增长的学习负担和赶课时的进度不足以让一线老师有足够的时间倾听。我认为如何解决这一现象可能才是专家们真正应该关注的。 杜威先生曾提出:情境-问题-分析-解决-验证。第一步是教师创设真实的问题情境;第二步是情境中蕴含刺激思维的问题;第三步是通过分析信息,提出假设;第四步是学生根据假设设计问题解决方案;第五步是通过实践检验假设的正确性。教育的第一性原理就是学生的学习规律。学习设计要指向深度理解,有助于学生之间平等协作、互相倾听、合作探究。学习设计要有助于学生的自主探索,学生在有趣且富有挑战性的问题引领下不断自主寻找答案。
平面和平面平行的性质定理ppt … 教学日期: 年月日 š 课题: 8.5.2 直线与平面平行(2)性质定理 – 普通高中教科书 数学 必修 第二册 8.5.2 直线与平面平行(2) 性质定理 第1张图片中的文字: 普通高中教科书 数学 必修 第二册 8.5.2 直线与平面平行(2) 性质定理 第2张图片中的文字: 教学日期: 年月 日 课题: 8.5.2直线与平面平行2) 目的: 理解并掌握线5平面平行的性质定理,强化线面平行使用条件 教学过程: 温知新,线面平行判定理 思考: 若a与b平行,则a内有多少条直线与b平行?无数条 追问: 若l与a平行,则a内有多少条直线都与l平行?不一定 思考: 若a与b平行,再添加什么条件让这条直线c与直线a平行?过直线作平面B,与平面›𘤺䯼Œ得到直线b,b与a平行 性质定理: 一条直线与一平面平行,则经过这条直线的平面与该平面相交得到的直线,和该直线平行 第3张图片中的文字: 课题: 教学日期: 年月日 如图E为PD中点C面PAD_BC=A 证:GAD 12)Ct面PAB 证限:(DC面PAD B 平是? BCL面AR 与面PAD友线是? 面PADA面ABCD=AD 12):分析:取PA中点E连搜.E C面PRCELBCE 例2.四锥S-ABCD中底面OD为,点E是SA上一点 当需为何值,S/面EPD) 过直线C确症一个平面与面 相交有一条友线,由性质应理,SC 与面EBD有多 SAC面EBD=. 由于0是Ae中点,E以是SA中点,那= 解当=E为SA中点 连接友BD点连E 底面D为 D为中点 第4张图片中的文字: 教学日期: 年月日 日 课题: E为SA中点 SC 若上为Be中点,当S面Enp SE ? EO面EBD面EBD SA CCIL面ERD 小结:判断线线平过方泛的了一条线面平行性质应理 关键在确定过已知直线的平面与知平面友线 = 求证: 证明b A本户 →alL acQ bEp ang=b 变述] A=1 求证:l 证照:过直线a作平面交面以子直线m AL llm dndi=m 词理,作平面使, !LA . an mln 由倒2可知,nnl all 第5张图片中的文字: 教学日期: 课题: 年 4在正方BD-ABCD中面AD和B 中作-面BC 7o1 M 应该如何作愿因? E 解过点P作MNIBC过点区作 A B 连接MEiNE 迹面为面MEFN 分过点.仅截面以和ABLCD有条过点P 友线 由子B面且面 C与该衣线过点P)平行数作MNLBC
二十四小时打一字
关于礼的作文
送医院锦旗
我要做好孩子
闺蜜生日祝福语
宣传部工作计划
幼儿园园务计划
家中趣事作文
怦然心动的感觉
为你点赞作文
餐饮员工管理制度
战略合作协议范本
很甜的小短句
噼里啪啦怎么写
打乒乓球作文
叙述文作文
妈妈的唠叨
高考励志
初中随笔
人生读书笔记
生意好的祝福语
现代企业管理制度
长辈生日
工伤事故报告模板
写夏天的作文
关于乡愁的古诗
保护地球的倡议书
我最喜欢的水果
学生意见怎么写
关于月的诗
心路历程怎么写
教学实施报告
出纳实操
人物品质的成语
兰亭集序教案
购车协议
收获作文800字
我得到了锻炼
写春天的景色作文
班级寄语
小班健康领域教案
难忘的端午节作文
培根随笔
我为学校代言
斗鸡赛
幼儿成长记录
调查报告的格式
作文盼
想对你说
安全检查简报
运营总监职责
只是因为那个人
关于成长的文章
儿童故事三只小猪
爱国英雄
从小事做起作文
岗位调动申请书
在回家的路上
校本培训心得体会
形容惊讶的成语
关于航天的作文
表示数量多的成语
细品人生路上的
难忘的一节课作文
小数乘法教案
感恩妈妈
行政专员岗位职责
美作文
我的童年趣事作文
写给朋友的一封信
活着阅读感悟
美术课堂教学
abac式的成语
观音心经全文
爸爸妈妈的话
我心中的榜样
公租房申请
有趣的一堂课
办公室岗位职责
自我介绍小学生
新年祝福贺词
护士简历模板
工程测量实习总结
运动会接力赛作文
辞职书怎么写
友谊让生活更美好
激情校园春色
人生感语
小孩子生日祝福语
驻村日志
试用期转正
三打白骨精的故事
结构化面试真题
我爱跑步
抗疫作文
贺卡祝福语
我的航天梦作文
友情破裂
调查研究心得体会
英语卷子家长评语
购物好评
严峻的近义词
凝聚作文600字
工作日志内容
公司考勤制度
女人不易
黄鹤楼的故事
成吉思汗的简介
质量分析会
工作失职检讨书
我的日记
考试评价
乌鸦与狐狸的故事
我是一个女生
读书日记怎么写
学校口号
安全教育大班
诚信名言名句
形容雨的诗句
英语谜语
我对自己说的寄语
小学运动会方案
榜样的作文
秋天丰收的古诗
写鸟的诗句
鼓励的句子
动物作文500字
介绍怎么写
歌颂友情的诗句
自古多情
关于交友的诗句
关于惜时的诗句
关于拼搏的句子
描写仙人掌的作文
我想变成孙悟空
转租合同模板
施工方法
珍惜粮食的手抄报
兔子的名片
关于青年的素材
善良的魅力
数与形教学反思
名人演讲
金融营销
何为感恩作文
护士工作
代表发言
重阳祝福
最美瞬间
我回来了
运动会美文
可能性的教学设计
考试作文600字
希望渺茫
写事的日记
客户经理岗位职责
勤能补拙的议论文
一路风景
本手妙手俗手作文
冷作文
给同学的毕业赠言
海上历险记
生孩子朋友圈
习作续写故事
监控合同范本
门卫保安岗位职责
雪作文
作文亲情
英语大学自我介绍
激情的五月
听课心得
拇指姑娘故事
霸气的个性签名
日落即景
写人作文六百字
长辈生日祝福语
树的作文
防汛抗旱工作总结
愿你一切都好
歌声嘹亮
保密承诺书
我的田园
十岁生日致辞
和平作文
美在路上
与祖国同行
个人计划
我们的运动会
质量承诺书
关于苏轼的作文
他和它
感情好的句子
关于交朋友的名言
秋天在哪里作文
珍爱生命名人名言
名人小故事有哪些
护士检讨书
车祸赔偿协议书
令人感动的事
读书分享心得体会
最新视频列表

玩转中点!仅需一道题,轻松学会“中点”的极致运用! #数学思维 #数学竞赛 #小学奥数 #小升初数学 #每日一题 抖音

阿基米德折弦定理:一个圆中一条由两长度不同的弦组成的折弦所对的两段弧的中点在较长弦上的射影,就是折弦的中点.哔哩哔哩bilibili

语文专试的中点抖音

二次函数二次函数图象上点的性质 #二次函数图象上点的性质 #二次函数图象 #二次函数图象和性质 #二次函数 抖音

五年级数学图形面积计算:学会利用图形性质巧算 20、图中平行四边形面积是48平方厘米,A是底边的中点,求涂色部分面积?#五年级数学图形题 抖音

中线长定理,三角函数重要结论.见到一边中点就可以用中线长定理.学生讲解,不好勿喷,谢谢哔哩哔哩bilibili

表面是关于中点知识点的6大考点之一"斜边中线"...初中阶段几何求最小值通常只有"2点间线段最短"和"垂线段最短"两个方式,而且该题其实最难的点...

平行四边形中点四边形 #中点四边形 #中点四边形性质 #平行四边形 抖音
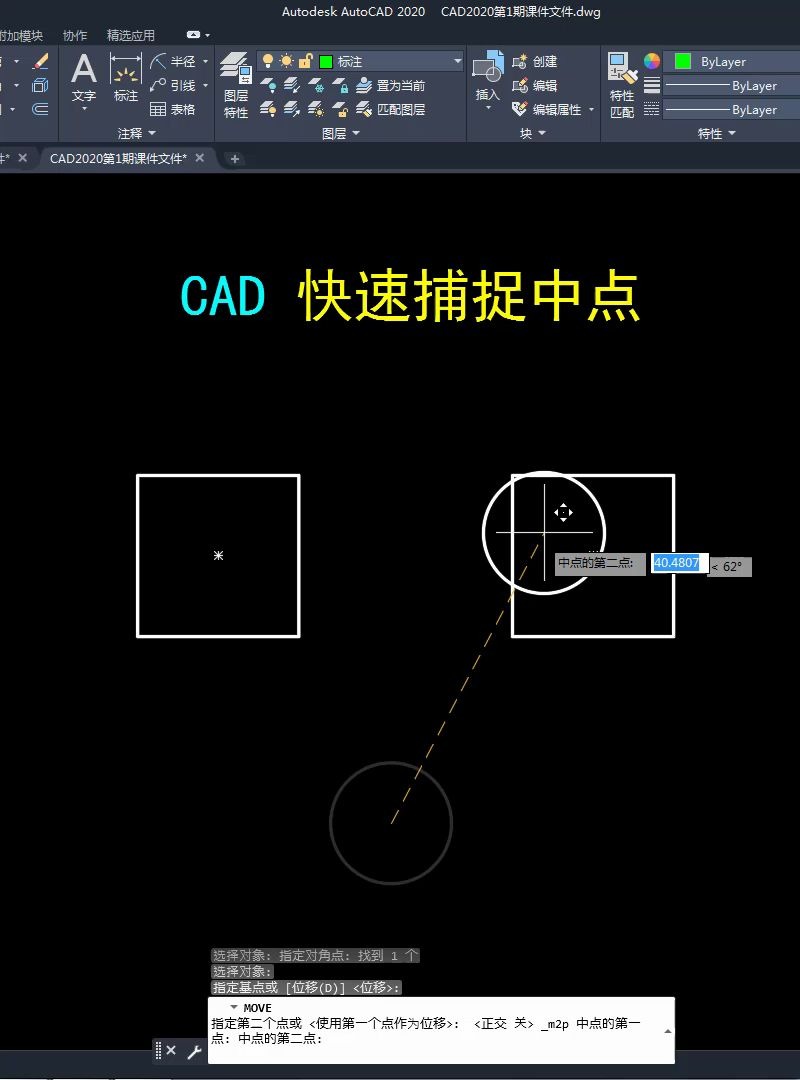
CAD技巧|CAD两点之间的中点的快速指定方法哔哩哔哩bilibili

小数的性质
最新素材列表
相关内容推荐
专栏内容推荐
- 素材来自:v.qq.com
- 初中数学中几何“中点问题”七大模型 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 720 x 862 · jpeg
- 中点四边形 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 1920 x 1920 · png
- 中点及其性质_百度百科
- 素材来自:baike.baidu.com
- 536 x 334 · png
- 直角梯形腰的中点性质-百度经验
- 素材来自:jingyan.baidu.com
- 619 x 397 · jpeg
- 中点相关的几何解法探究 | 数学吧
- 素材来自:maths8.com
- 600 x 587 · jpeg
- 中点四边形 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 871 x 1039 · jpeg
- 中点四边形 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 1280 x 720 · jpeg
- 初中数学:利用中点和勾股定理的性质,构造方程式,轻松解题_腾讯视频}
- 素材来自:v.qq.com
- 4217 x 2769 · jpeg
- 圆锥曲线中的几个定值(一) - 知乎
- 素材来自:zhuanlan.zhihu.com
- 650 x 487 · jpeg
- 中线和中点的性质
- 素材来自:photoint.net
- 640 x 676 · jpeg
- 哪些定理或性質與三角形的中點有關?會有哪些常見經典考試題型? - 每日頭條
- 素材来自:kknews.cc
- 800 x 448 · jpeg
- 平行四边形性质-初二数学基础题,阴影面积的求法,中点的性质,教育,学校教育,好看视频
- 素材来自:haokan.baidu.com
- 800 x 320 · jpeg
- 线段中点的性质_初三网
- 素材来自:chusan.com
- 1595 x 1801 · jpeg
- 平面几何定理之七(三角形中位线定理) - 知乎
- 素材来自:zhuanlan.zhihu.com
- 679 x 841 · jpeg
- 八省联考一道圆锥曲线求面积问题(利用中点的性质求面积) - 知乎
- 素材来自:zhuanlan.zhihu.com
- 1019 x 514 · jpeg
- 中考数学|遇三角形一边垂线过这边中点,考虑用垂直平分线的性质 - 哔哩哔哩
- 素材来自:bilibili.com
- 1303 x 638 · png
- 计算机图形学02:中点BH算法绘制直线_图形学直线绘制-CSDN博客
- 素材来自:blog.csdn.net
- 600 x 413 · png
- 三角形中线的性质
- 素材来自:wenwen.sogou.com
- 1272 x 1748 · png
- 椭圆中点弦的两个有趣性质及应用_word文档在线阅读与下载_免费文档
- 素材来自:mianfeiwendang.com
- 920 x 1303 · png
- 节梯形的性质定理梯形两腰中点连线定理梯形的两腰中点
- 素材来自:zhuangpeitu.com
- 640 x 327 · jpeg
- 初中必会几何中点四大模型之四:斜边中点连中线(口诀突破)
- 素材来自:k.sina.cn
- 1354 x 770 · jpeg
- 密克点的一个性质 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 502 x 387 · png
- 三角形中三条中线的交点叫什么点_初三网
- 素材来自:chusan.com
- 1080 x 810 · jpeg
- 三角形中位线判定方法-三角形中位线定理逆定理-三角形中位线和中线的区别
- 素材来自:sx.ychedu.com
- 600 x 365 · jpeg
- 中考数学|遇三角形一边垂线过这边中点,考虑用垂直平分线的性质 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 560 x 416 · jpeg
- 初中数学三角形全等的判定+性质+辅助线技巧都在这里了!考前必看 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 710 x 279 · jpeg
- 调和点列的定义、基本性质与简单应用 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 1080 x 810 · jpeg
- 梯形的性质判定-梯形中位线定理-梯形的周长与面积
- 素材来自:sx.ychedu.com
- 1577 x 644 · jpeg
- 调和点列的定义、基本性质与简单应用 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 800 x 450 · jpeg
- 三角形中点连线的性质 - 生活百科 - 微文网
- 素材来自:wenvx.com
- 640 x 409 · jpeg
- 中考数学七大模型——总有一款你的最爱 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 794 x 447 · jpeg
- 北师大版九年级上册3 正方形的性质与判定完美版课件ppt-教习网|课件下载
- 素材来自:51jiaoxi.com
- 860 x 1216 · png
- [数学]初中数学60个几何模型专题复习:模型1 双中点模型(含答案)-试卷下载预览-二一课件通
- 素材来自:doc.21cnjy.com
- 600 x 271 · jpeg
- 北师大版初中数学九年级上册成比例线段与比例的基本性质公开课优质课课件教案视频 - 知乎
- 素材来自:zhuanlan.zhihu.com
随机内容推荐
广州奥林匹克中学
憋组词
二次三项式
折射率公式
many比较级
哎图片
热带季风气候分布
化学专业有哪些
现实主义作品
索尼清朝大臣
嫉妒的成语
解姓氏怎么读
弹性模量计算
一个米一个更
鹤峰一中
李端端图
lazy反义词
耳的偏旁
蜻蜓队长是谁
雨是怎么来的
吾得兄事之
定风波柳永
曹州武校
三土念什么
海拔和气温的关系
三角形的高的公式
韩国人平均身高
语言描写作用
牛的重量
分类别的作用
教师入党动机
化简的方法
辛弃疾摸鱼儿
割席断交的翻译
鞭的部首
工作部门怎么填
时髦的意思
太原到五台山
爱迪生的发明
玫瑰和金鱼读后感
磁通量的单位
上课走神怎么办
蒙眬的意思
氮气会爆炸吗
英语疑问句的结构
中国有几所大学
一氧化碳的毒性
g5420
三字明星
形容写字好的成语
临猗中学
串联和并联的特点
wear的过去式
人生鼎沸的意思
春秋争霸的实质
宝鸡石油中学
高三一模考试时间
利润率的公式
as倒装句的用法
立方的计算公式
石组词有哪些
幂函数的单调性
皇帝制度的特点
贵州安顺学院
弹力的作用点
哈姆雷特人物
郸城一中
中华大字典
胸的组词
1696年
离骚的艺术成就
黄金计划软件
不止和不只
zhu四声组词
集合的表示方法
三线合一的性质
大连铁路卫生学校
葸
邓稼先的贡献
滑稽英文
王子
沈阳市第十七中学
鲁智深介绍
高三多大
治国有常
如懿传大阿哥
飞机上能带水果吗
大气压强是多少
天道结局
最大政治优势
invite名词
所以是什么意思
花荣的主要事迹
1米有多长
自然天成的意思
事业编面试
纪念什么意思
宋香
辅酶和辅基
班会结束语
飞行员视力
东江大桥在哪里
赣榆智贤中学
宅邸读音
离散系数怎么算
大召寺简介
公元纪年法的来历
醉花间冯延巳
青铜葵花主要内容
古代骂人的话
智慧团建团员登录
魅是什么意思
关系副词有哪些
径流是什么意思
夫学须静也
宵旰
渭南高级中学
积极分子下一步
一个火一个宣
学分有什么用
离岗退养政策
中文系大学排名
cny什么意思
mangoes
位移电流密度
什么叫幂
偶数可以是负数吗
大连招生考试网
四个水是什么字
二战开始时间
长信秋词王昌龄
两个向量相乘
天官赐福花城
朝花夕拾每章概括
晋中教育网
a包含于b符号
梅岭音乐节
热带海洋性气候
生硬是什么意思
夙夜在公
stop过去式
表示递进的关联词
地理现象
分数乘小数怎么算
here的中文
一什么路
晚春感事陆游
脸字组词
河北区号是多少
过秦论的中心论点
发挥党员作用
司空图二十四诗品
恐龙用英语怎么说
正方体英语
承载是什么意思
自勉联
山东美术联考时间
四时田园杂兴拼音
折射率计算公式
发挥党员
东莞实验技工学校
除法有分配律吗
swim过去分词
皆是什么意思
形容词物主代词
专科上几年
武汉最好的大学
stock翻译
钢琴十级需要几年
东江大桥在哪里
高职什么意思
冒昧打扰
横钩的字有哪些
法家思想主张
语文动词有哪些
恒德高中
林子祥个人资料
3月4号
维明路小学
葡萄糖结构
教师职业道德论文
违背是什么意思
春秋三传是什么
our音标
翅的部首
洋务运动的特点
天海佑希身高
嵩县实验中学
it的反身代词
举文言文意思
美术有哪些专业
空客32a
西北省份有哪些
儒家五经
密度的物理意义
最大无关组怎么求
圣诞节翻译
登封旅游景点大全
fear翻译
四川中学排名
今日热点推荐
羽绒服敢卖199赌的就是你不懂
凌晨六点是警惕性最低的时间
湾区生活又又又又又又提速了
先人一步 活得漂亮
男子47万买3手宾利发现竟是13手
冬天身上痒1天洗2次澡反患湿疹
警方回应小米su7外借却被拍色情片
吉利星主播
傅首尔说能get到麦琳的点
鹤岗迎破纪录特大暴雪
东北女生在南方被冻到怀疑人生
塔克拉玛干沙漠被整个围起来了
鹿晗凌晨直播与粉丝连麦
父母希望黄圣依有正常的婚姻关系
特朗普关税大棒下没有赢家
辨别真假羽绒服的小技巧
大冰为脑瘫女孩追星薛之谦
鹿晗直播
Newjeans宣布解约
再见爱人节目组发声明
孔刘刘仁娜同框
丁禹兮看自己的物料考古直播
突然发现国内夫妻很少见戴婚戒
马 你骑我出来最好是有天大的事
孕妇坠崖案当事人谈男子推妻坠海骗保
麦琳全职妈妈带两娃的KPI被忽视
黄圣依回应父母对其婚姻的态度
广州地铁通报5人因下车拥挤冲突
卢布崩了
网约车司机双胞胎女儿考入清北
易烊千玺评论区回复王俊凯王源
贺峻霖接手向太轮椅
梁洪源当爸
拿千元羽绒服翻新拆开竟没有羽绒
儿子牺牲后妈妈还能收到他的信
胖东来每件羽绒服都标有进货价
GimGoon回应Doinb队出局
遭前男友囚禁烫伤女生脱离生命危险
首付3万买了没人要的阁楼
还有2个月就是除夕了
华晨宇 果然人在尴尬时会很忙
斯瓦泰克兴奋剂阳性
俄罗斯卢布跌超8.5
梅艳芳 拜拜
河南杂技夫妻相继发生高空坠落背后
猎罪图鉴2下周播出
民警猥亵继女案开庭女孩勇敢出庭
丈夫住院取2.5万元被银行电话核实
志愿军老兵为战友吹响冲锋号
曼联3比2博德闪耀
DNA音乐节
车企付款周期大比拼
【版权声明】内容转摘请注明来源:http://seo.07yue.com/2lgtz84_20241129 本文标题:《中点的性质前沿信息_中点的性质是什么(2024年11月实时热点)》
本站禁止使用代理访问,建议使用真实IP访问当前页面。
当前用户设备IP:18.222.44.156
当前用户设备UA:Mozilla/5.0 AppleWebKit/537.36 (KHTML, like Gecko; compatible; ClaudeBot/1.0; +claudebot@anthropic.com)